P01G2015 – Average Velocity
Average Velocity
You drive east for a distance of $75\ km$ at a speed $20\ m/s$ and then drive $50\ km$ west at a speed $30\ m/s$.
1. What is your average velocity? Give direction and magnitude.
View answerHide answer
By definition, the average velocity vector is equal to
{\overrightarrow{v}}_{avg}=\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}where $\mathrm{\Delta }\overrightarrow{r}$ is the displacement vector. Here, the net displacement is $\mathrm{\Delta }\overrightarrow{r}=25\ km\ \overrightarrow{x}$ and the time $\mathrm{\Delta }t$ is the sum of the time for each portion i.e.
\mathrm{\Delta }t=t_1+t_2=\frac{\mathrm{\Delta }x_1}{v_1}+\frac{\mathrm{\Delta }x_2}{v_2}where $t_1$ is the time spent traveling the distance $\mathrm{\Delta }x_1$ at speed $v_1$ and $t_2$ is the time spent traveling the distance $\mathrm{\Delta }x_2$ at speed $v_2$. The average velocity vector is therefore equal to
\boxed{{\overrightarrow{v}}_{avg}=\frac{\mathrm{\Delta }\overrightarrow{r}}{\displaystyle{\frac{\mathrm{\Delta }x_1}{v_1}+\frac{\mathrm{\Delta }x_2}{v_2}}}=\frac{25\cdot {10}^3}{\displaystyle{\frac{75\cdot {10}^3}{20}+\frac{50\cdot {10}^3}{30}}}\overrightarrow{x}\approx 4.62\ m/s\ \overrightarrow{x}}2. Suppose you now drive $75\ km$ east at a speed $20\ m/s$ then drive $50\ km\ $north at $30\ m/s$. What is your average velocity? Give magnitude and direction.
View answerHide answerIn this case the displacement vector is drawn below
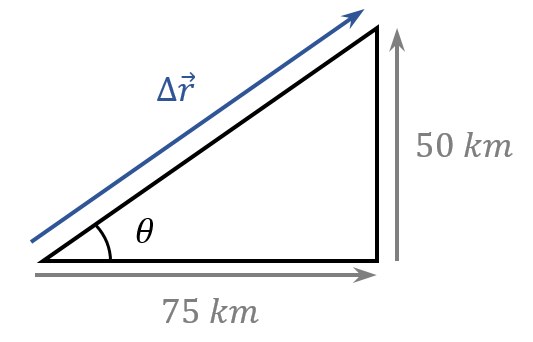
and its magnitude is given by the Pythagorean Theorem and is equal to
\left|\mathrm{\Delta }\overrightarrow{r}\right|=\sqrt{{75}^2+{50}^2}\approx 90.1\ kmThe average velocity vector therefore has magnitude
\boxed{\left|{\overrightarrow{v}}_{avg}\right|=\left|\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}\right|=\frac{90.1\cdot {10}^3}{\displaystyle{\frac{75\cdot {10}^3}{20}+\frac{50\cdot {10}^3}{30}}}\approx 16.63\ m/s}The direction of the average velocity vector is given by the angle $\theta $ and we have
{\mathrm{tan} \left(\theta \right)\ }=\frac{50}{75}=\frac{2}{3}\ \ \ \ \ \Rightarrow \ \ \ \ \ \ \boxed{\theta ={{\mathrm{tan}}^{-1} \left(\frac{2}{3}\right)\ }\approx 33.7{}^\circ}The average velocity points $33.7{}^\circ \ $above the horizontal (North of East).
