P02G2018 – Air Drop
Air Drop
A plane, diving at an angle of $37{}^\circ $ below the horizontal, releases a projectile at an altitude of $730\ m$. At the moment of release, the projectile and plane are traveling in the same direction at the same speed. The projectile hits the ground $5.0\ s$ after release.
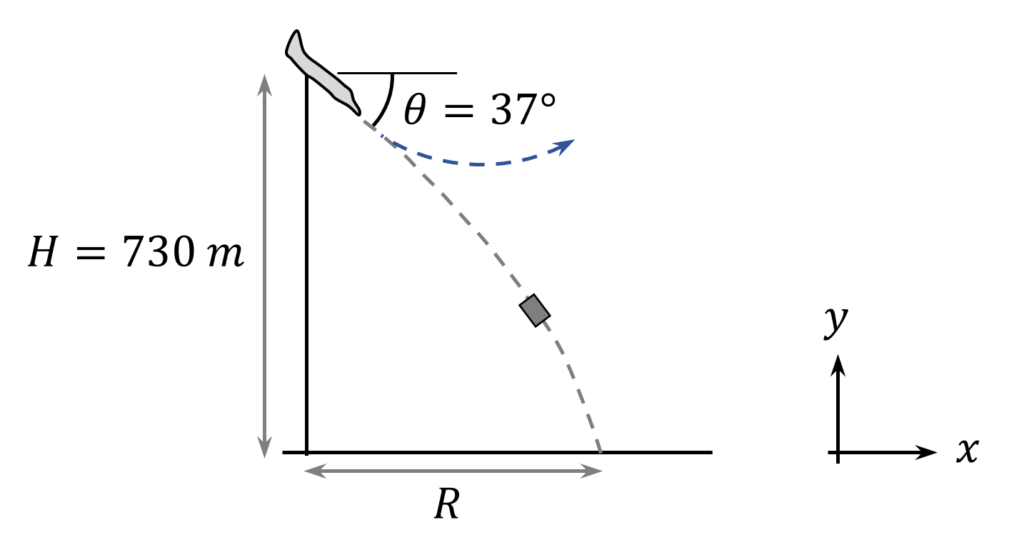
1. What was the speed of the plane?
View answerHide answerWe let $v_0$ denote the speed of the plane and $t_1$ denote the time at which the projectile hits the ground.
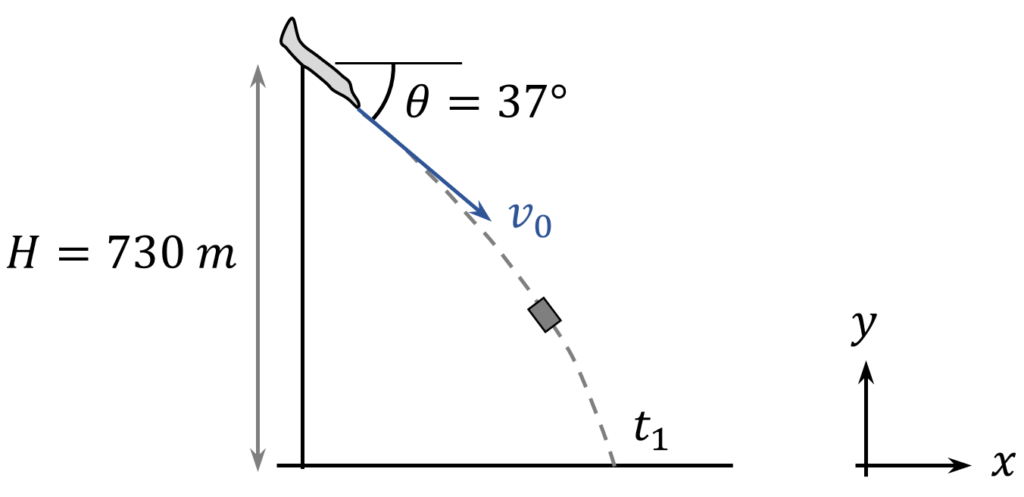
The kinematic equations of the projectile, after being released at $t=0$, are
\left\{ \begin{array}{c}
x\left(t\right)=v_0{\mathrm{cos} \left(\theta \right)\ }t \\
v_x\left(t\right)=v_0{\mathrm{cos} \left(\theta \right)\ } \end{array}
\right.\ \ \ \ \ \ \ \ \ \ \ \ and\ \ \ \ \ \ \ \ \ \ \ \ \left\{ \begin{array}{c}
\displaystyle{y\left(t\right)=-\frac{1}{2}gt^2-v_0{\mathrm{sin} \left(\theta \right)\ }t+H} \\
v_y\left(t\right)=-gt-v_0{\mathrm{sin} \left(\theta \right)\ } \end{array}
\right.At time $t_1=5.0\ s$, the projectile reaches the ground and therefore $t_1$ satisfies $y\left(t_1\right)=0$. We then solve for $v_0$ as follows
\begin{aligned}
y\left(t_1\right)=0\ \ \ \ &\Rightarrow \ \ \ \ -\frac{1}{2}gt^2_1-v_0{\mathrm{sin} \left(\theta \right)\ }t_1+H=0 \\
&\Rightarrow \ \ \ \ \ v_0{\mathrm{sin} \left(\theta \right)\ }t_1=H-\frac{1}{2}gt^2_1 \\
&\Rightarrow \ \ \ \ \ v_0=\frac{\displaystyle{H-\frac{1}{2}gt^2_1}}{{\mathrm{sin} \left(\theta \right)\ }t_1}
\end{aligned}Thus, the speed of the plane is equal to
\boxed{v_0=\frac{\displaystyle{H-\frac{1}{2}gt^2_1}}{{\mathrm{sin} \left(\theta \right)\ }t_1}-\frac{\displaystyle{730-\frac{1}{2}\cdot 10\cdot 5^2}}{{\mathrm{sin} \left(37\right)\ }\cdot 5}\approx 202\ m/s}2. How far does the projectile travel horizontally during its flight?
View answerHide answerThe horizontal distance traveled by the projectile in the time $t_1$ is equal to
\boxed{R=x\left(t_1\right)=v_0{\mathrm{cos} \left(\theta \right)\ }t_1=202\cdot {\mathrm{cos} \left(37\right)\ }\cdot 5\approx 807\ m}3. What is the speed and direction of motion of the projectile just before hitting the ground? Express direction as an angle below the horizontal.
View answerHide answerThe projectile hits the ground with a velocity ${\overrightarrow{v}}_1$ that has components $v_x\left(t_1\right)$ and $v_y\left(t_1\right)$ as shown below
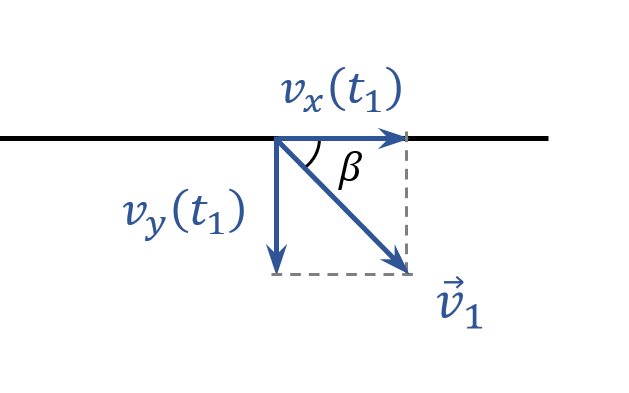
The components are equal to
\begin{aligned}
v_x\left(t_1\right)&=v_0{\mathrm{cos} \left(\theta \right)\ }=202\cdot {\mathrm{cos} \left(37\right)\ }\approx 161.3\ m/s \\
v_y\left(t_1\right)&=-gt_1-v_0{\mathrm{sin} \left(\theta \right)\ }=-9.8\cdot 5-202\cdot {\mathrm{sin} \left(37\right)\ }\approx -170.6\ \ m/s
\end{aligned}The speed of the projectile when it hits the ground is therefore equal to
\boxed{v_1=\sqrt{v_x{\left(t_1\right)}^2+v_y{\left(t_1\right)}^2}=\sqrt{{161.3}^2+{\left(-170.6\right)}^2}\approx 235\ \ m/s}The direction of the velocity ${\overrightarrow{v}}_1$ is given by the angle $\beta $ which can be computed as follows
{\mathrm{tan} \left(\beta \right)\ }=\frac{v_y\left(t_1\right)}{v_x\left(t_1\right)}\ \ \ \ \ \Rightarrow \ \ \ \ \ \boxed{\beta ={{\mathrm{tan}}^{-1} \left(\frac{v_y\left(t_1\right)}{v_x\left(t_1\right)}\right)\ }={{\mathrm{tan}}^{-1} \left(-\frac{170.6}{161.3}\right)\ }\approx -46.6{}^\circ}The projectile hits the ground at an angle $\beta \approx 46.6{}^\circ $ below the horizontal.
