P02R2017 – Hats Off to Frosty
Hat’s Off to Frosty
Frosty is enjoying a cold sunny day, idly standing in the snow. A child throws a snowball of mass $m=0.25\ kg$ from an initial height $H=2\ m$ at Frosty. The snowball is thrown with initial velocity $v_0=20\ m/s$ at an angle $\theta =30{}^\circ $. Frosty’s hat is located at a height $H$ with respect to the ground. You may use $g\approx 10\ m/s^2$.
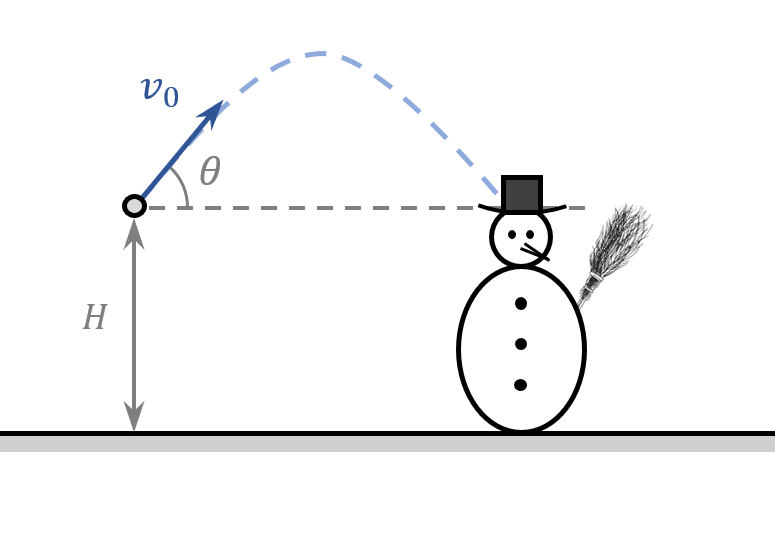
Given:
{\mathrm{cos} \left(30\right)\ }=\frac{\sqrt{3}}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathrm{sin} \left(30\right)\ }=\frac{1}{2}1. What are the components $a_x$ and $a_y$ of the acceleration of the snowball?
View answerHide answerDuring the time the snowball is airborne, the components of its acceleration are
\boxed{
\left\{ \begin{array}{c}
a_x=0 \ \ \ \\
a_y=-g \end{array}
\right.
}2. Derive the kinematic equations $x\left(t\right)$ and $y\left(t\right)$ of the snowball.
View answerHide answerThe snowball is launched from the initial position $\displaystyle{\left\{ \begin{array}{c}
x_0=0 \\
y_0=H \end{array}
\right.}$ and the components of its initial velocity are $v_{0x}=v_0{\mathrm{cos} \left(\theta \right)\ }$ and $v_{0y}=v_0{\mathrm{sin} \left(\theta \right)\ }$. The kinematic equations describing the flight of the snowball are therefore
\boxed{
\left\{ \begin{array}{c}
x\left(t\right)=v_0{\mathrm{cos} \left(\theta \right)\ }t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
\\
\displaystyle{y\left(t\right)=-\frac{1}{2}gt^2+v_0{\mathrm{sin} \left(\theta \right)\ }+H} \end{array}
\right.\ \ \ \ \ \ \ \ \ \ and\ \ \ \ \ \ \ \ \ \ \left\{ \begin{array}{c}
v_x\left(t\right)=v_0{\mathrm{cos} \left(\theta \right)\ } \\
\\
v_y\left(t\right)=-gt+v_0{\mathrm{sin} \left(\theta \right)\ } \end{array}
\right.
}3. What is the maximum height reached by the snowball? Where ($x$ location) does it reach its maximum height?
View answerHide answer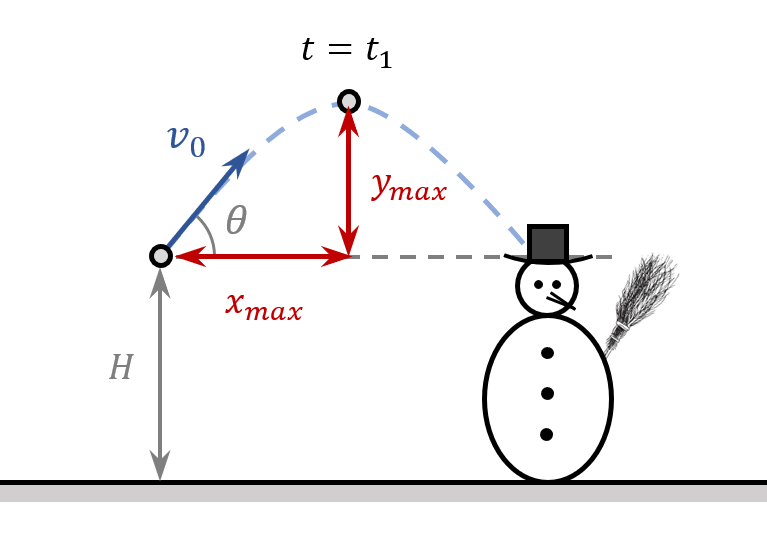
The snowball reaches its maximum height at time $t_1$ such that $v_y\left(t_1\right)=0$ and we therefore solve for $t_1$ as follows
\begin{aligned}
v_y\left(t_1\right)=0\ \ \ \ &\Rightarrow \ \ \ \ -gt_1+v_0{\mathrm{sin} \left(\theta \right)\ }=0 \\
\\
&\Rightarrow \ \ \ \ \ t_1=\frac{v_0{\mathrm{sin} \left(\theta \right)\ }}{g} \\
\\
&\Rightarrow \ \ \ \ \ t_1=\frac{\displaystyle{20\cdot \frac{1}{2}}}{10}= 1 \ s
\end{aligned}Its maximum height is then given by
\boxed{y_{max}=y\left(t_1\right)=-\frac{1}{2}gt^2_1+v_0{\mathrm{sin} \left(\theta \right)\ }t_1+H=-\frac{1}{2}\cdot 10\cdot 1^2+20\cdot \frac{1}{2}\cdot 1+2=7\ m}The $x$-location of the snowball when it reaches it maximum height is equal to
\boxed{x_{max}=x\left(t_1\right)=v_0{\mathrm{cos} \left(\theta \right)\ }t_1=20\cdot \frac{\sqrt{3}}{2}\cdot 1=10\sqrt{3}\ m}4. What is the speed of the snowball when it is at its maximum height?
View answerHide answer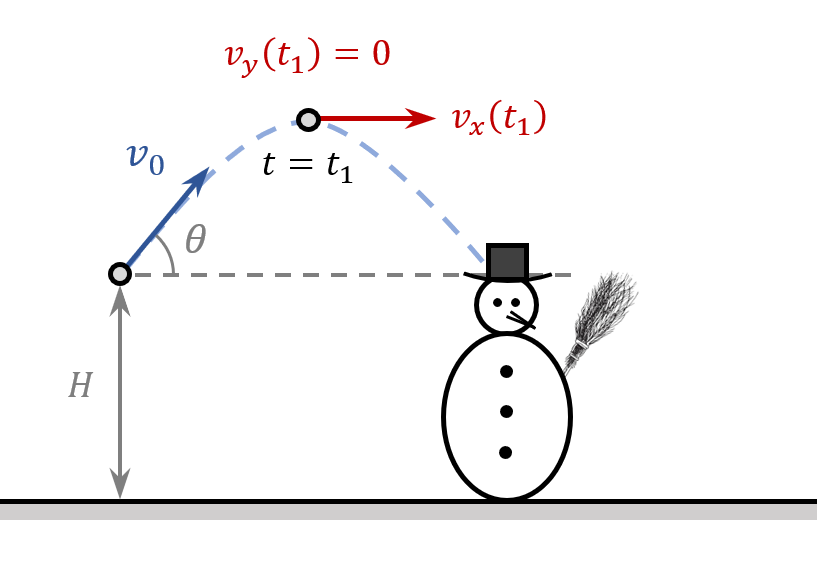
The $y$-component of the snowball’s velocity is zero when it reaches its maximum height and therefore the speed of the snowball is then equal to
\boxed{v_{top}=\sqrt{v_x{\left(t_1\right)}^2+v_y{\left(t_1\right)}^2}=v_x\left(t_1\right)=v_0{\mathrm{cos} \left(\theta \right)\ }=10\sqrt{3}\ \ \ m/s}5. Assuming that the snowball knocks off Frosty’s hat, how far is the child from Frosty?
View answerHide answer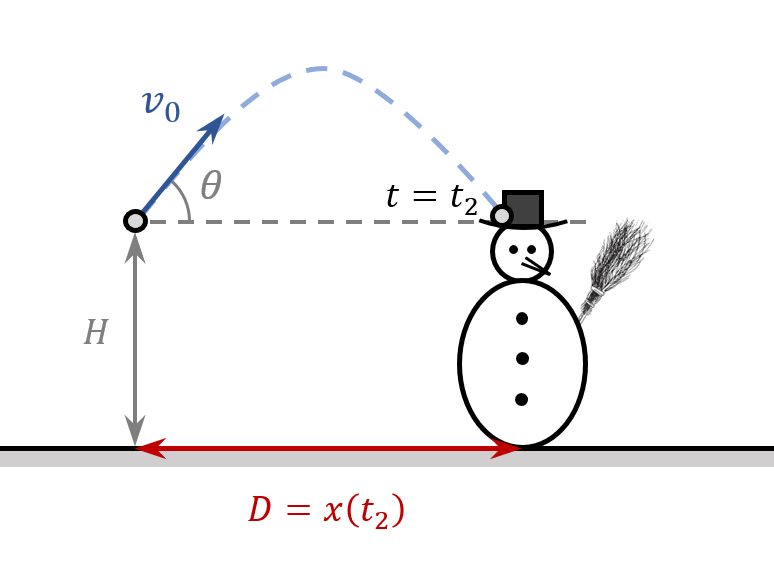
The snowball reaches Frosty’s hat at time $t_2$ such that $y\left(t_2\right)=H$ and we solve for $t_2$ as follows
\begin{aligned}
y\left(t_2\right)=H\ \ \ \ &\Rightarrow \ \ \ \ -\frac{1}{2}gt^2_2+v_0{\mathrm{sin} \left(\theta \right)\ }t_2+H=H \\
\\
&\Rightarrow \ \ \ \ -\frac{1}{2}gt^2_2+v_0{\mathrm{sin} \left(\theta \right)\ }t_2=0 \\
\\
&\Rightarrow \ \ \ \ \ t_2\left(-\frac{1}{2}gt_2+v_0{\mathrm{sin} \left(\theta \right)\ }\right)=0 \\
\\
&\Rightarrow \ \ \ \ \ t_2=0\ \ \ \ \ or\ \ \ \ -\frac{1}{2}gt_2+v_0{\mathrm{sin} \left(\theta \right)\ }=0 \\
\\
&\Rightarrow \ \ \ \ \ t_2=0\ \ \ \ \ or\ \ \ \ \ t_2=\frac{2v_0{\mathrm{sin} \left(\theta \right)\ }}{g}
\end{aligned}Ruling out $t_2=0$, we conclude the snowball reaches Frosty’s hat at time $t_2$ equal to
t_2=\frac{2v_0{\mathrm{sin} \left(\theta \right)\ }}{g}=\frac{\displaystyle{2\cdot 20\cdot \frac{1}{2}}}{10}=2\ sThe distance $D$ between the child and Frosty is equal to the distance traveled by the snowball in time $t_2$ and is given by
\boxed{D=x\left(t_2\right)=v_0{\mathrm{cos} \left(\theta \right)\ }t_2=20\cdot \frac{\sqrt{3}}{2}\cdot 2=20\sqrt{3}\ \ m}