P01G2019 – Cars Racing Alongside Each Other
Cars Racing Alongside Each Other
At $t=0$, two cars are racing alongside one another. One car is traveling at $20\ m/s$ and is speeding up at a rate of $1.5\ m/s^2$, while the other is traveling in the same direction at $30\ m/s$ and is slowing down at a rate of $1\ m/s^2$.
1. How far will they travel before they are alongside one another again?
View answerHide answer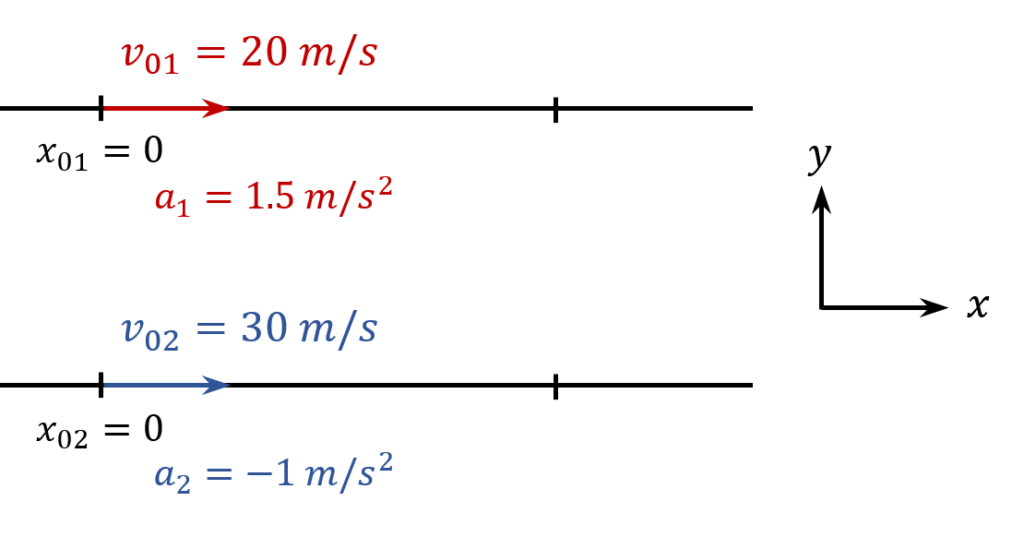
Car 1 has an initial velocity of $v_{01}=20\ m/s$, an acceleration $a_1=1.5\ m/s^2$, and an initial position $x_{01}=0$. Its kinematic equations are therefore
\left\{ \begin{array}{c}
\displaystyle{x_1\left(t\right)=\frac{1}{2}a_1t^2+v_{01}t} \\
\\
v_1\left(t\right)=a_1t+v_{01} \end{array}
\right.Car 2 has an initial velocity of $v_{02}=30\ m/s$, an acceleration $a_2=-1\ m/s^2$, and an initial position $x_{02}=0$. Its kinematic equations are therefore
\left\{ \begin{array}{c}
\displaystyle{x_2\left(t\right)=\frac{1}{2}a_2t^2+v_{02}t} \\
\\
v_2\left(t\right)=a_2t+v_{02} \end{array}
\right.The cars are alongside when $x_1\left(t\right)=x_2\left(t\right)$ i.e.
\begin{aligned}
x_1\left(t\right)=x_2\left(t\right)\ \ \ \ &\Rightarrow \ \ \ \ \frac{1}{2}a_1t^2+v_{01}t=\frac{1}{2}a_2t^2+v_{02}t \\
\\
&\Rightarrow \ \ \ \ \ t\left(\left(\frac{1}{2}a_1-\frac{1}{2}a_2\right)t+\ v_{01}-v_{02}\right)=0 \\
\\
&\Rightarrow \ \ \ \ \ t=0\ \ \ \ \ or\ \ \ \ \ t=\frac{{2(v}_{02}-v_{01})\ }{a_1-a_2}
\end{aligned}Ruling out the time $t=0$, we conclude that the cars are alongside again at time
t=\frac{{2(v}_{02}-v_{01})\ }{a_1-a_2}=\frac{2\left(30-20\right)}{1.5-\left(-1\right)}=8\ sThus, the distance they will have traveled in that time is equal to
\boxed{x_1\left(t\right)=x_2\left(t\right)=\frac{1}{2}a_2t^2+v_{02}t=\frac{1}{2}\left(-1\right)\cdot 8^2+30\cdot 8=208\ \ m}2. What will be their relative speed when they are alongside one another again?
View answerHide answerCar 1 will be moving at speed
\boxed{v_1\left(t\right)=a_1t+v_{01}=1.5\cdot 8+20=32\ m/s}Car 2 will be moving at speed
\boxed{v_2\left(t\right)=a_2t+v_{02}=-1\cdot 8+30=22\ m/s}Their relative speed when they are alongside one another again will be equal to
\boxed{v_1\left(t\right)-v_2\left(t\right)=32-22=10\ m/s}