P01R2015 – Components & Dot Product
Components & dot product
Consider the vectors ${\overrightarrow{v}}_1$ and ${\overrightarrow{v}}_2$ drawn below.

1. Using trigonometry, find the components of ${\overrightarrow{v}}_1$. Take ${\theta }_1=30{}^\circ $ and $v_1=5\ m/s$.
View answerThe magnitude of the components of ${\overrightarrow{v}}_1$ can be derived by considering the sine and the cosine of ${\theta }_1$ based on the figure below
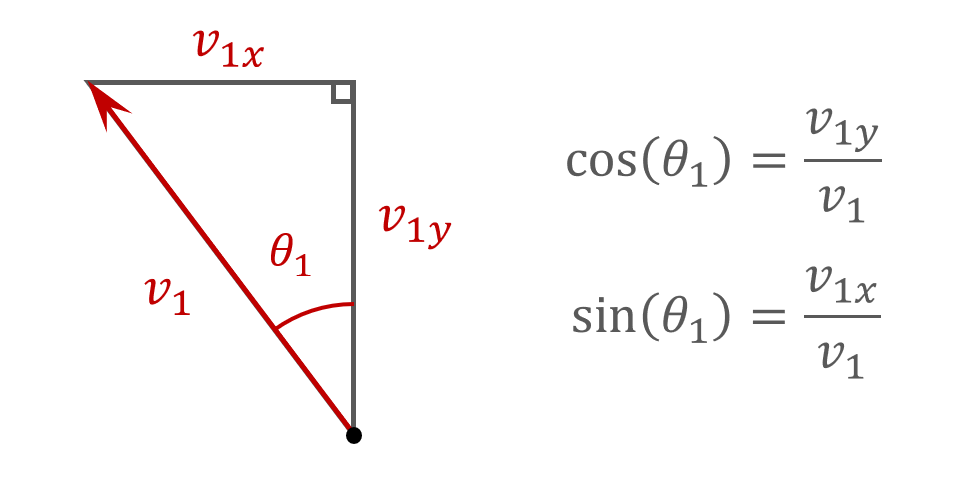
By definition, we have
\begin{aligned}
{\mathrm{cos}\left({\theta }_1\right)\ }&=\frac{v_{1y}}{v_1}\ \ \ \ \Rightarrow \ \ \ \ \ v_{1y}=v_1{\mathrm{cos} \left({\theta }_1\right)\ }\\
\\
{\mathrm{sin}\left({\theta }_1\right)\ }&=\frac{v_{1x}}{v_1}\ \ \ \ \Rightarrow \ \ \ \ \ v_{1x}=v_1{\mathrm{sin} \left({\theta }_1\right)\ }
\end{aligned}Noting that the $x$ component of ${\overrightarrow{v}}_1$ is in fact negative (as it points left), we conclude that the components of ${\overrightarrow{v}}_1$ are
\boxed{
\begin{aligned}
v_{1x}&=v_1{\mathrm{sin} \left({\theta }_1\right)\ } \approx -2.50 \ m/s \\
\\
v_{1y}&=v_1{\mathrm{cos} \left({\theta }_1\right)\ }\approx 4.33 \ m/s
\end{aligned}
}2. Using the dot product, find the components of ${\overrightarrow{v}}_2$. Take ${\theta }_2=-40{}^\circ $ and $v_2=4\ m/s$.
View answerThe $x$-component of ${\overrightarrow{v}}_2$ is derived by computing the dot product of ${\overrightarrow{v}}_2$ with $\hat{x}$ which has magnitude $\left|\hat{x}\right|=1$. The angle between ${\overrightarrow{v}}_2$ and $\hat{x}$ is ${\theta }_2$ and we therefore conclude that $v_{2x}$ is equal to
\boxed{v_{2x}={\overrightarrow{v}}_2\cdot \hat{x}=v_2\cdot 1\cdot {\mathrm{cos} \left({\theta }_2\right)\ }=4\cdot {\mathrm{cos} \left(-40\right)\ }\approx 3.06\ \ m/s}The $y$-component of ${\overrightarrow{v}}_2$ is derived by computing the dot product of ${\overrightarrow{v}}_2$ with $\hat{y}$ which has magnitude $\left|\hat{y}\right|=1$. The angle between ${\overrightarrow{v}}_2$ and $\hat{y}$ is $90-{\theta }_2$ and we therefore conclude that $v_{2y}$ is equal to
\boxed{v_{2y}={\overrightarrow{v}}_2\cdot \hat{y}=v_2\cdot 1\cdot {\mathrm{cos} \left({90-\theta }_2\right)\ }=4\cdot {\mathrm{cos} \left(90+40\right)\ }\approx -2.57\ \ m/s}3. Consider the acceleration vector $\overrightarrow{a}$ that makes an angle ${\theta }_3$ with respect to the $x$-axis as shown below. Find the magnitude of $\overrightarrow{a}$ and the angle ${\theta }_3$ from the given components $a_x$ and $a_y$.

The magnitude of the acceleration $\overrightarrow{a}$ is given by the Pythagorean Theoreom and is equal to
\boxed{\left|\overrightarrow{a}\right|=\sqrt{a^2_x+a^2_y}=\sqrt{2^2+3^2}\approx 3.60\ m/s^2}To determine the angle ${\theta }_3$, we write ${\mathrm{tan} \left({\theta }_3\right)\ }$ as follows which yields
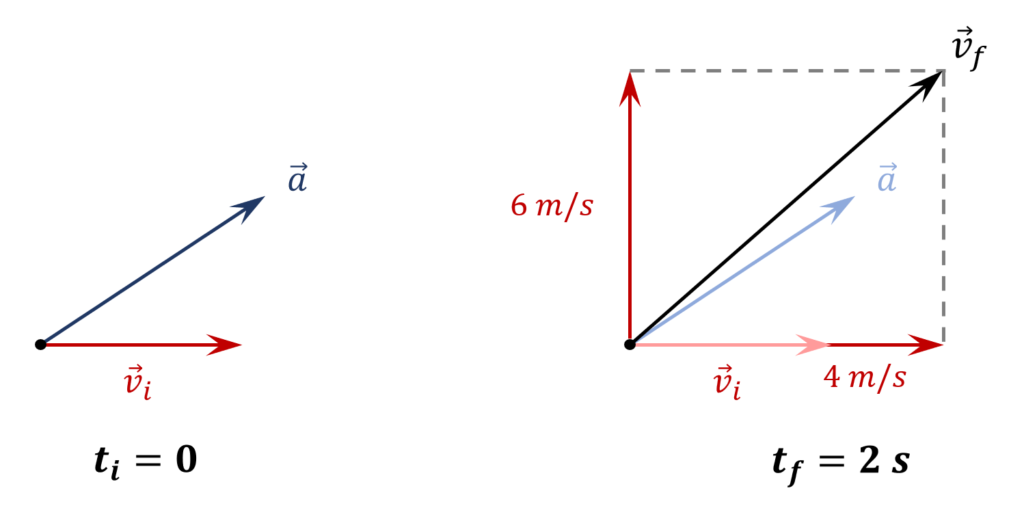
{\mathrm{tan} \left({\theta }_3\right)\ }=\frac{a_y}{a_x}\ \ \ \ \Rightarrow \ \ \ \ \ \boxed{{\theta }_3={{\mathrm{tan}}^{-1} \left(\frac{a_y}{a_x}\right)\ }={{\mathrm{tan}}^{-1} \left(\frac{3}{2}\right)\ }\approx 56.30{}^\circ}4. What would the effect of $\overrightarrow{a}$ be on a horizontal velocity vector ${\overrightarrow{v}}_i$ with magnitude $3\ m/s$ over a period $\mathrm{\Delta }t=2\ s$? Assume that the acceleration vector $\overrightarrow{a}$ is constant in magnitude and direction.
View answerThe horizontal component of the acceleration $\overrightarrow{a}$ is $a_x=2\ m/s^2$. This means that the horizontal velocity will increase by $2\ m/s$ every second and therefore over a period of $\mathrm{\Delta }t=2\ s$, a horizontal velocity vector would increase by $4\ m/s$.
The vertical component of the acceleration $\overrightarrow{a}$ is $a_y=3\ m/s^2$. This means that the vertical velocity will increase by $3\ m/s$ every second and therefore over a period of $\mathrm{\Delta }t=2\ s$, a horizontal velocity vector would increase by $6\ m/s$ in the vertical direction.