P01R2015 – Catching the Bus
Catching the Bus
The bus you take to work is a distance $D=25\ m$ from your bus stop and you are a distance $d=15\ m$ away behind the bus. The bus has an initial velocity $v_{0B}=10\ m/s$ and is decelerating with $a_B=-2m/s^2$. It waits for $t^*=10\ s$ at the bus stop before leaving. You are running at your constant maximum speed $v_{max}=5\ m/s$ initially. As shown below, choose the origin for $x$ to be at the bus stop.
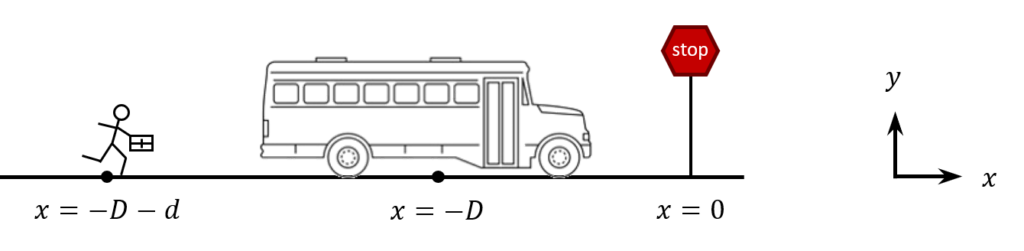
1. Setup the kinematic equations $x\left(t\right)$ and $v_x\left(t\right)$ for the bus and you.
View answer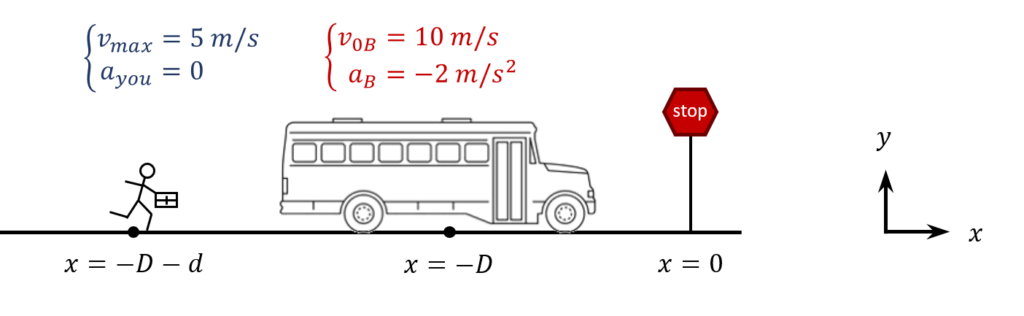
The kinematic equations that describe your motion are
\left\{ \begin{array}{c}
\displaystyle{x_{you}\left(t\right)=x_0+v_{0x}t+\frac{1}{2}a_xt^2=-\left(D+d\right)+v_{max}t} \\
\\
v_{x\ you}\left(t\right)=v_{0x}+a_xt=v_{max} \end{array}
\right.The kinematic equations that describe the motion of the bus are
\left\{ \begin{array}{c}
\displaystyle{x_B\left(t\right)=-D+v_{0B}t+\frac{1}{2}a_Bt^2} \\
\\
v_{x\ B}\left(t\right)=v_{0B}+a_Bt \end{array}
\right.2. What is the speed of the bus at time $t_1=2\ s$? At $t_2=5\ s$?
View answerThe speed of the bus at time $t_1=2\ s$ is equal to
\boxed{v_{x\ B}\left(t_1\right)=v_{0B}+a_Bt_1=10-2\cdot 2=6\ m/s}The speed of the bus at time $t_2=5\ s$ is equal to
\boxed{v_{x\ B}\left(t_2\right)=v_{0B}+a_Bt_2=10-2\cdot 5=0\ m/s}Thus, we conclude that the bus comes to a stop at time $t_2$ exactly.
3. What is the distance between you and the bus at time $t_1=2\ s$?
View answerThe position of the bus at time $t_1=2\ s$ is equal to
x_B\left(t_1\right)=-D+v_{0B}t_1+\frac{1}{2}a_Bt^2_1=-25+10\cdot 2-\frac{1}{2}\cdot 2\cdot 2^2=-9\ mYour position at time $t_1=2\ s$ is equal to
x_{you}\left(t_1\right)=-\left(D+d\right)+v_{max}t_1=-25-15+5\cdot 2=-30\ mThe distance between you and the bus at time $t_1$ is therefore equal to
\boxed{x_{you}\left(t_1\right)-x_B\left(t_1\right)=-30-\left(-9\right)=-21\ m}4. How long does it take you to reach the bus stop? Can you catch the bus?
View answerYou reach the bus stop at time $t$ such that $x_{you}\left(t\right)=0$ and we solve for $t$ as follows
\begin{aligned}
x_{you}\left(t\right)=0\ \ \ &\Leftrightarrow \ \ \ \ \ -\left(D+d\right)+v_{max}t=0 \\
\\
&\Leftrightarrow \ \ \ \ \ t=\frac{D+d}{v_{max}}
\end{aligned}Thus, you reach the bus stop after running an amount of time $t$ equal to
\boxed{t=\frac{D+d}{v_{max}}==\frac{25+15}{5}=8\ s}The bus reaches the stop after $t_2=5\ s$ (from question 2.) and waits there $10\ s$. This gives $15\ s$ to reach the bus stop which is you enough time to catch the bus.
